Lobotomizing some models

TLDR:

Using metaheuristics to prune layers from AI while mainting model performance.

Introduction

I have been reading about how current LLMs are too big. The current trend shows that Small Language Models (SLM) are just getting better and better. Look at Moondream or in a not so small format Llama3.3 70b that is as good as the 405b model.

So, how could we make current models smaller? We can remove parts of it. Models are like onions, they have layers.

There are some layers that are more important than others¹. We don’t need all of them, so, we could remove some of the layers and still have a good enough model. Using a benchmark as a proxy to determine which models are good and which ones are bad. But, I am as the kids say, GPU poor. So to approach this problem, I had do it without a lot of compute.

The paper from Sakana Labs about Evolutionary Model Merging inspired this idea. The main concept behind this paper is that by using evolutionary algorithms you can merge two different models and get optimal new LLMs. The authors were not sure which amount of a model was more important than the other one. But at the end of the day Evolutionary Algorithms are a good way to search through the possible combinations and get good enough new model. The important thing in here is that you can get a good new model only by evaluating models. Through evolution alone, they were able to merge two fine-tuned model one for Japanese and another one for math into a single model that excelled at both tasks.

But before we can apply it, I need to explain a bit more about the problem.

Search space

Depending on the model size, the search space can be small, but it can get out of hand. If we want to test different models with different amounts of activated layers. How should we do that in the first place?

For example, we have two different states for any given model, where they can have an on or off layer (0 or 1). For small models, let’s say Llama-1B, we have 16 different LlamaDecoderLayers. This gives us a total of 2¹⁶ different possible combinations for layers either to keep or throwaway. And I am sorry, I am not going to be testing a total of 65,536 different possible combinations of models. And that is for a super tiny model of 1B parameters. If We compare it to something bigger like Qwen2.5-32B. We get 2⁶⁴ combinations which is a total of 18446744073709600000 possible models. There are more possible model combinations than grains of sand on Earth². So no, I am not going to be brute forcing this.

Instead of bruteforcing we are going to be searching.

Metaheuristics to the rescue

We could get the BEST solution if we were to brute force all the solution space. But, we can do a trade off. We can apply a metaheuristic and get a decent solution in resonable time.

Also, after some trial and error I realized that the middle layers where not that important³. So I created an init that biases into that.

def create_individual(gene_length: int) -> List[int]:
    """
    Creates an individual with bias towards keeping outer layers and being more
    selective with middle layers. Uses a quadratic function to create a
    probability distribution that's higher at the edges and lower in the
    middle.
    """
    individual = []
    
    # Parameters to control the shape of the probability curve
    edge_prob = 0.9  # Probability of keeping edge layers
    middle_prob = 0.4  # Probability of keeping middle layers
    
    for i in range(gene_length):
        # Convert position to range [-1, 1] where 0 is the middle
        x = (2 * i / (gene_length - 1)) - 1
        
        # Quadratic function that's higher at edges (-1 and 1) and lower in middle (0)
        # p(x) = ax^2 + b where a and b are chosen to match our desired probabilities
        a = (edge_prob - middle_prob)
        b = middle_prob
        prob = a * x * x + b
        
        # Create gene based on calculated probability
        individual.append(1 if random.random() < prob else 0)
    
    # Force keeping first and last layers (optional, but often beneficial)
    if gene_length > 2:  # Only if we have more than 2 layers
        individual[0] = 1  # Keep first layer
        individual[-1] = 1  # Keep last layer
    
    return individual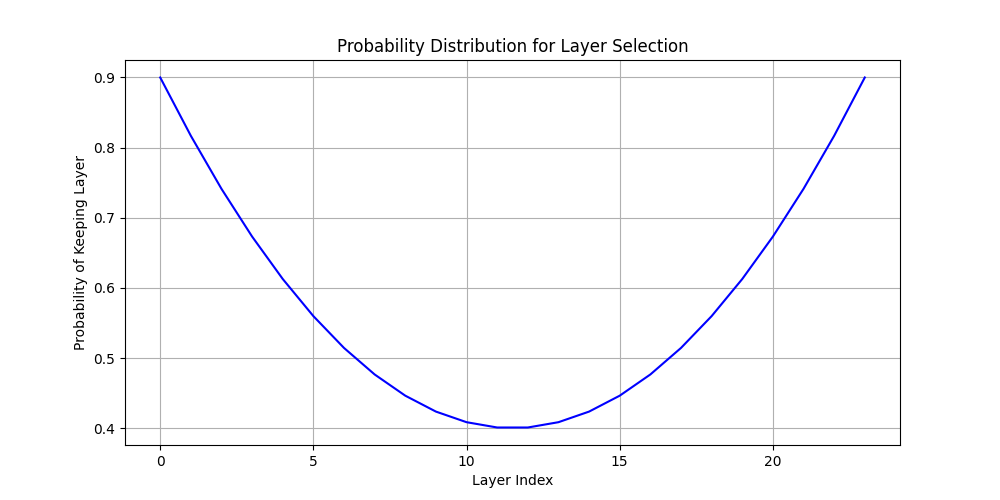

But we have to test this models against something. So I decided to go with tinyBenchmarks. Specifically, just for this testing I went with tinyMMLU They are a good proxy for bigger benchmarks. Although it is not the real deal, we want to test a lot of models, so they should do for now.

Finally, as for the algorithms, I decided on three different ones. Hill Climbing with restarts, Simulated Annealing and Simple Genetic Algorithms. Each algorithm has its pros and cons, all need a bit more testing but after initial experiments I can tell you that:

• Hill Climbing: This algorithm focuses only on trying to find local maximums. I paired it up with a lot of restarts so that it could select multiple initial states. But it still needs more movement, it got stuck on local maximums and never improved.

• Simulated Annealing: This algorithms is better against getting stuck in local maximums. It battles local maximums by having a temperature that can make it choose worse values to incentivise search.

• Genetic Algorithms: You use a population, you breed them and make them have random mutations. Overall, it was the best approach even if it ended up cycling for a little bit.

I tested locally with Qwen/Qwen2.5-0.5B and for a bit beefier benchmarks I used NousHermes/Llama-3-8B and Qwen/Qwen2.5-32B-Instruct.

The best method is Genetic Algorithms thanks to the diverse layer configurations. Second place went to Simulated Annealing. In last place there is Hill Climbing⁴ stuck in local maximums.

Vibe check failure

Even though the models seemed to be competant at tests they were talking jiberish.

But in Compact Language Models via Pruning and Knowledge Distillation they said that after pruning the model they would finetune it and get better results.

And after adding finetuning into the pipeline the models where a bit better, and could finally talk again. I went with Open-Orca/SlimOrca as the dataset and with only 200 steps, the models were talking again.

Almost all models got a healthy bump after the finetune.

Scaling a bit more

I wanted to scale a bit more. So I decided to test Qwen2.5-32B-Instruct in an H100.

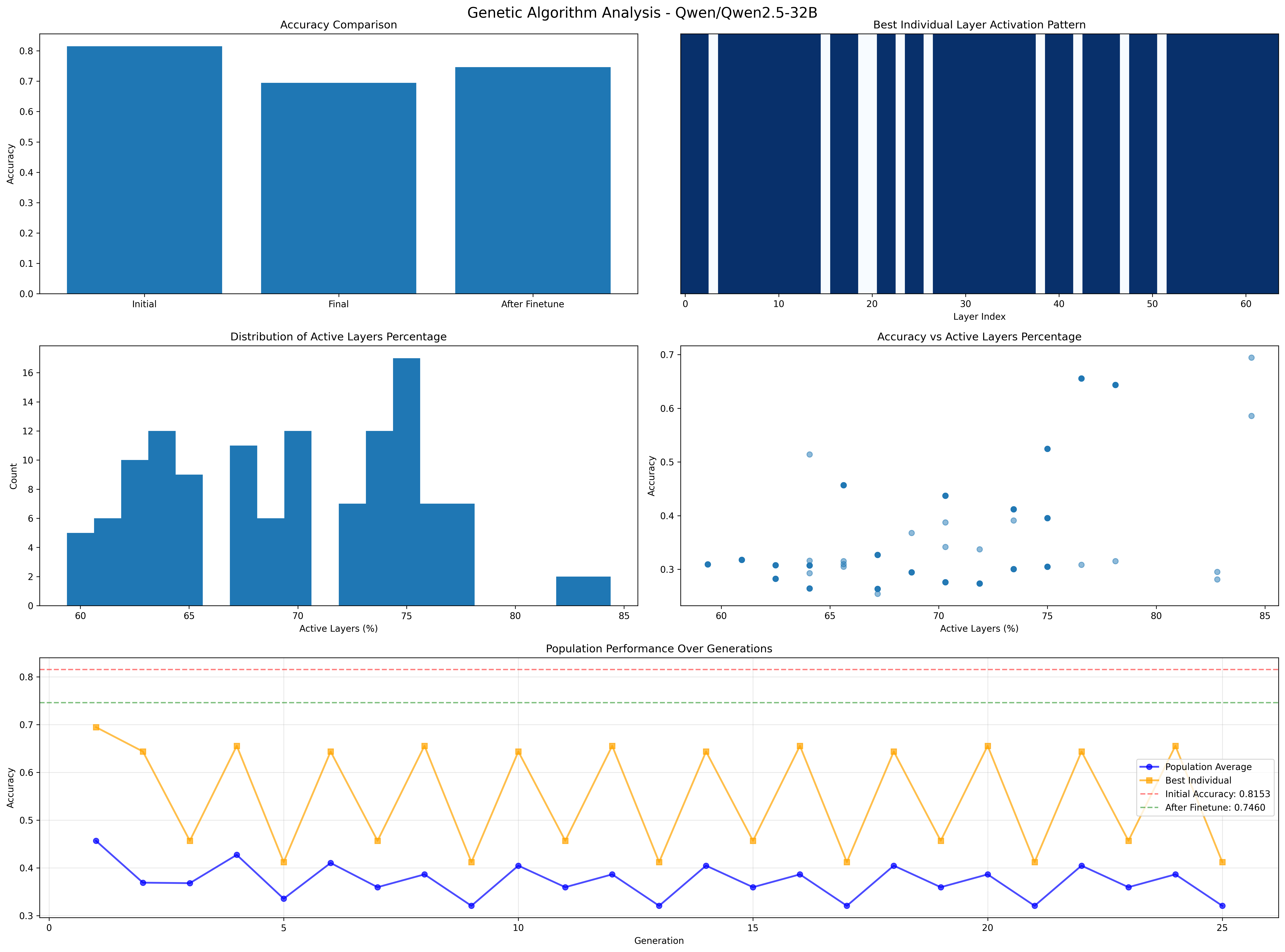
The original score from the model was 81.5% and it went down to 74.6%, a reduction of 6.9% but the model has 28.12% less parameters. I would say that this was a success. Although, it seems that Simple Genetic Algorithms seem to still have been stuck in a local optima.

Conclusion

I liked planning this problem and solving around my constraints. I do think that you could do more research in this area and get a better algorithm for this. I will be doing a round 2 with other Derivative-free Optimizers and maybe even publish a paper because I like the direction where this is going.

Finally, it would be pretty interesting to see the pareto frontier for different amounts of layers.

If you want to read the code, it is public on Github right here. Also, the different configs for the different models are in the RESULTS directory.

Acknowledgements

I would like to thank Ciaran for listening to all of my ideas while developing this project. He provided code for mixing layers that was a pretty good starting point for developing all of the metaheuristics.

Footnotes

---

1. If you want to read about it you can read about at Compact Language Models via Pruning and Knowledge Distillation↩︎

2. As per NPR there are 7.5 x 10^18 grains of sand by this article.↩︎

3. I still need to do further research into this. This specific function worked better on some runs for the Genetic Algorithms so that’s why I endedup deciding on it.↩︎

4. I genuinely want to do a deeper dive into Hill Climbing but for now it is not working.↩︎

Back to articles